Trace
11.16 每日一题 完美矩形
传送门:https://leetcode-cn.com/problems/perfect-rectangle/
Problem
给你一个数组 rectangles ,其中 rectangles[i] = [xi, yi, ai, bi] 表示一个坐标轴平行的矩形。这个矩形的左下顶点是 (xi, yi) ,右上顶点是 (ai, bi) 。
如果所有矩形一起精确覆盖了某个矩形区域,则返回 true ;否则,返回 false 。
示例 1:
1
2
3
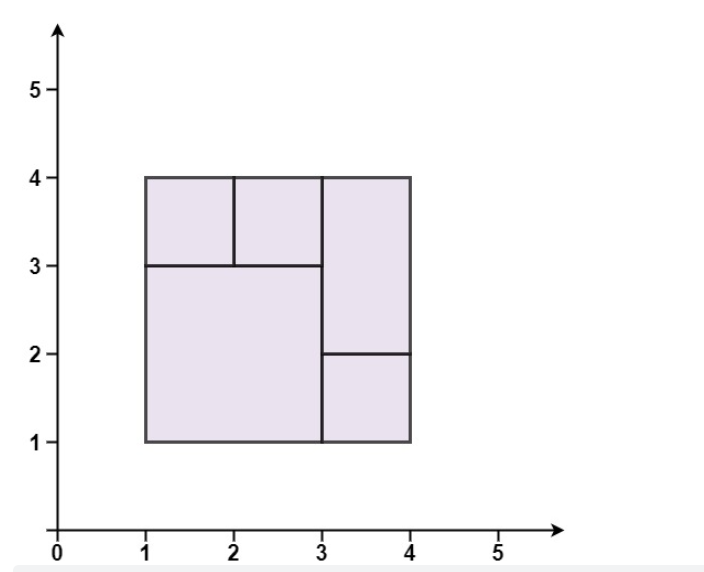
| 输入:rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
输出:true
解释:5 个矩形一起可以精确地覆盖一个矩形区域。
|
示例 2:
1
2
3
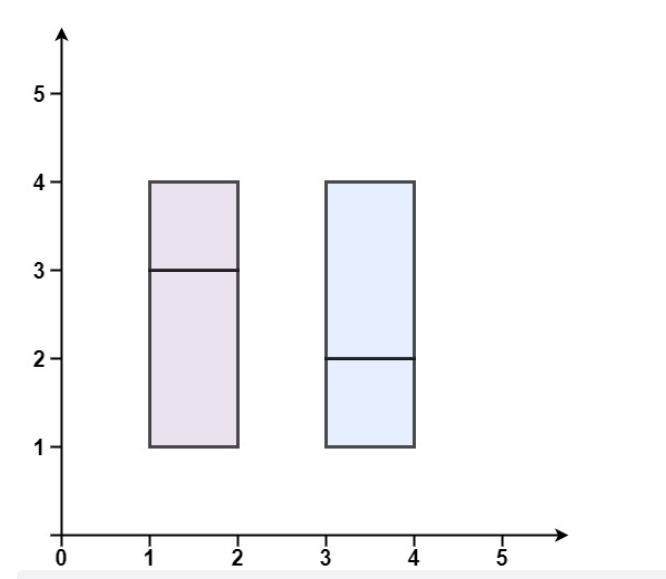
| 输入:rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
输出:false
解释:两个矩形之间有间隔,无法覆盖成一个矩形。
|
示例 3:
1
2
3
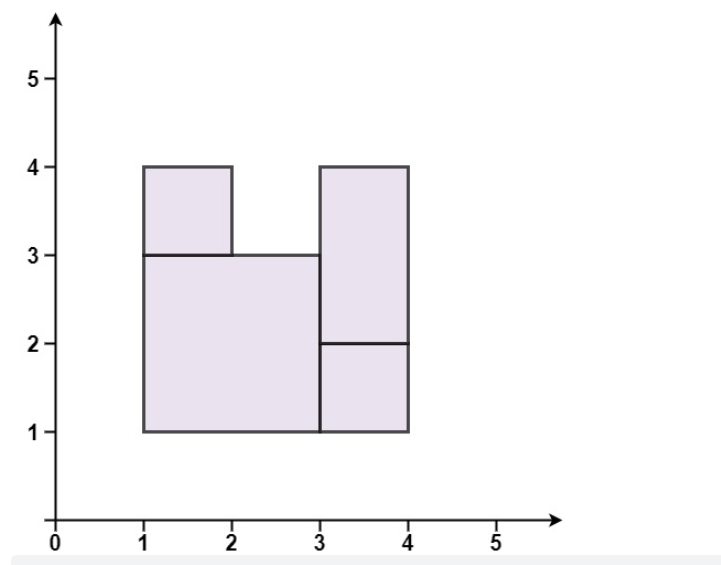
| 输入:rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[3,2,4,4]]
输出:false
解释:图形顶端留有空缺,无法覆盖成一个矩形。
|
示例 4:
1
2
3
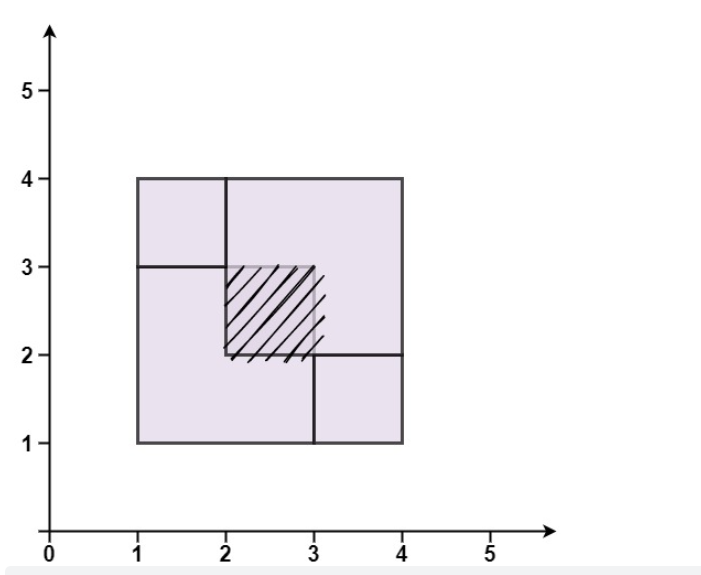
| 输入:rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]]
输出:false
解释:因为中间有相交区域,虽然形成了矩形,但不是精确覆盖。
|
提示:
1
2
3
| 1 <= rectangles.length <= 2 * 1e4
rectangles[i].length == 4
-1e5 <= xi, yi, ai, bi <= 1e5
|
方法一
观察样例找规律可知,完美矩形的充要条件为:拼接后得到的矩形面积等于所有矩形面积之和,图形中的顶点出现次数为2或4(大矩形的四个顶点为1除外)。
程序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| class Solution {
public:
map<pair<long long,long long>, int> times;
bool isRectangleCover(vector<vector<int>>& rectangles) {
long long sum_area=0;
long long minX=0x3f3f3f3f,minY=0x3f3f3f3f,maxX=-0x3f3f3f3f,maxY=-0x3f3f3f3f;
for(int i=0;i<rectangles.size();i++){
long long x1=rectangles[i][0],y1=rectangles[i][1],x2=rectangles[i][2],y2=rectangles[i][3];
minX=min(minX,x1);
minY=min(minY,y1);
maxX=max(maxX,x2);
maxY=max(maxY,y2);
sum_area+=(x2-x1)*(y2-y1);
times[{x1,y1}]++;
times[{x2,y2}]++;
times[{x1,y2}]++;
times[{x2,y1}]++;
}
if(sum_area!=(maxX-minX)*(maxY-minY)){
return false;
}
for(auto i:times){
if((i.first.first==minX&&i.first.second==minY)||(i.first.first==maxX&&i.first.second==maxY)||
(i.first.first==minX&&i.first.second==maxY)||(i.first.first==maxX&&i.first.second==minY)){
if(i.second!=1){
return false;
}
}
else if(i.second!=2&&i.second!=4){
cout<<i.first.first<<" "<<i.first.second<<endl;
cout<<i.second<<endl;
return false;
}
}
return true;
}
};
|
方法二(扫描线)
扫描线解法:
将每个矩形看成两条竖直方向的直线,以$(x,y1,y2,flag)$的格式存,$flag$区分矩形的左边还是右边;
每一条非边缘的竖线,左右两边一定成对存在;
每一条边缘的竖线,左或右只出现一次;
其中,对非边缘的竖线,可以由无缝拼接而成的竖线成对存在(ps,成对存在的线段在$y$方向上可以不相邻,因此对同一个$x$,可能需要存多个线段,然后一一匹配)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
| class Solution {
public:
vector<vector<int>> vt;
bool isRectangleCover(vector<vector<int>>& rectangles) {
int n=rectangles.size();
for(int i=0;i<n;i++){
vt.push_back({rectangles[i][0],rectangles[i][1],rectangles[i][3],0});
vt.push_back({rectangles[i][2],rectangles[i][1],rectangles[i][3],1});
}
sort(vt.begin(),vt.end());
int m=vt.size();
for(int l=0;l<m;){
int r=l;
while(r<m&&vt[r][0]==vt[l][0]){
r++;
}
vector<vector<int>> left;
vector<vector<int>> right;
for(int i=l;i<r;i++){
if(vt[i][3]==0){
vector<int> cur={vt[i][1],vt[i][2]};
if(left.empty()){
left.push_back(cur);
}
else{
if(left[left.size()-1][1]>cur[0]){
return false;
}
else if(left[left.size()-1][1]==cur[0]){
left[left.size()-1][1]=cur[1];
}
else{
left.push_back(cur);
}
}
}
else if(vt[i][3]==1){
vector<int> cur={vt[i][1],vt[i][2]};
if(right.empty()){
right.push_back(cur);
}
else{
if(right[right.size()-1][1]>cur[0]){
return false;
}
else if(right[right.size()-1][1]==cur[0]){
right[right.size()-1][1]=cur[1];
}
else{
right.push_back(cur);
}
}
}
}
if(l>0&&r<m){
if(left.size()!=right.size()){
return false;
}
else{
for(int j=0;j<left.size();j++){
if(left[j][0]!=right[j][0]||left[j][1]!=right[j][1]){
return false;
}
}
}
}
else{
if(left.size()==0&&right.size()==1||left.size()==1||right.size()==0){
}
else return false;
}
l=r;
}
return true;
}
};
|





