Trace
第264场周赛C 统计最高分的节点数目
传送门:https://leetcode-cn.com/problems/count-nodes-with-the-highest-score/
Problem
给你一棵根节点为 0 的 二叉树 ,它总共有 n 个节点,节点编号为 0 到 n - 1 。同时给你一个下标从 0 开始的整数数组 parents 表示这棵树,其中 parents[i] 是节点 i 的父节点。由于节点 0 是根,所以 parents[0] == -1 。
一个子树的 大小 为这个子树内节点的数目。每个节点都有一个与之关联的 分数 。求出某个节点分数的方法是,将这个节点和与它相连的边全部 删除 ,剩余部分是若干个 非空 子树,这个节点的 分数 为所有这些子树 大小的乘积 。
请你返回有 最高得分 节点的 数目 。
示例 1:
1
2
3
4
5
6
7
8
9
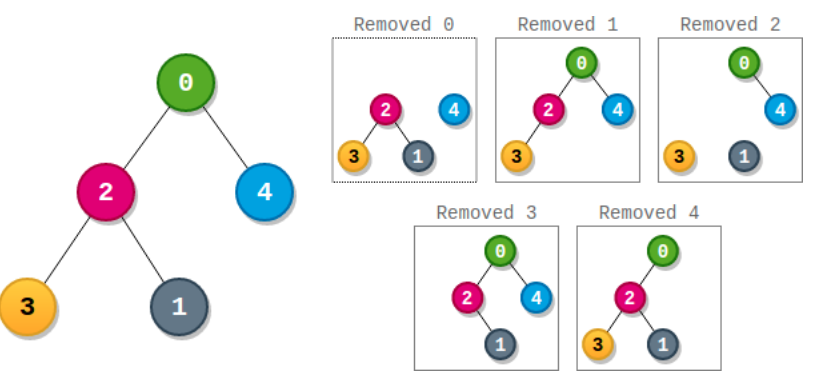
| 输入:parents = [-1,2,0,2,0]
输出:3
解释:
- 节点 0 的分数为:3 * 1 = 3
- 节点 1 的分数为:4 = 4
- 节点 2 的分数为:1 * 1 * 2 = 2
- 节点 3 的分数为:4 = 4
- 节点 4 的分数为:4 = 4
最高得分为 4 ,有三个节点得分为 4 (分别是节点 1,3 和 4 )。
|
示例 2:
1
2
3
4
5
6
7
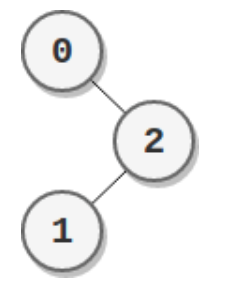
| 输入:parents = [-1,2,0]
输出:2
解释:
- 节点 0 的分数为:2 = 2
- 节点 1 的分数为:2 = 2
- 节点 2 的分数为:1 * 1 = 1
最高分数为 2 ,有两个节点分数为 2 (分别为节点 0 和 1 )。
|
提示:
n == parents.length2 <= n <= 1e5
parents[0] == -1
- 对于
i != 0 ,有 0 <= parents[i] <= n - 1
parents 表示一棵二叉树。
思路
对二叉树来说,删去某个点,最多形成三个连通分量,即左子树,右子树,以及剩下的部分。
可以先$dfs$一次,预处理出二叉树中以每个结点为根的子树的结点数量。
然后根据拆分后的情况求得分(是否存在左右子树,是否存在双亲结点/是否为$0$号结点)。
程序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| class Solution {
public:
long long ans=0;
int n;
int num=0;
int childnums[100010];
vector<vector<int>> child;
int dfs(int k){
if(child[k].size()==0){
childnums[k]=1;
return childnums[k];
}
for(int i=0;i<child[k].size();i++){
int u=child[k][i];
childnums[k]+=dfs(u);
}
childnums[k]++;
return childnums[k];
}
long long getScore(int k){
long long score=1;
if(n-childnums[k]>0){
score=n-childnums[k];
}
for(int i=0;i<child[k].size();i++){
int u=child[k][i];
score*=childnums[u];
}
return score;
}
int countHighestScoreNodes(vector<int>& parents) {
n=parents.size();
child=vector<vector<int>>(n);
for(int i=1;i<parents.size();i++){
child[parents[i]].push_back(i);
}
dfs(0);
for(int i=0;i<n;i++){
long long tmp=getScore(i);
if(tmp>ans){
num=1;
ans=tmp;
}
else if(tmp==ans){
num++;
}
}
return num;
}
};
|



