Trace
剑指 Offer II 112. 最长递增路径
传送门:https://leetcode-cn.com/problems/fpTFWP/
Problem
给定一个 m x n 整数矩阵 matrix ,找出其中 最长递增路径 的长度。
对于每个单元格,你可以往上,下,左,右四个方向移动。 不能 在 对角线 方向上移动或移动到 边界外(即不允许环绕)。
示例 1:
1
2
3
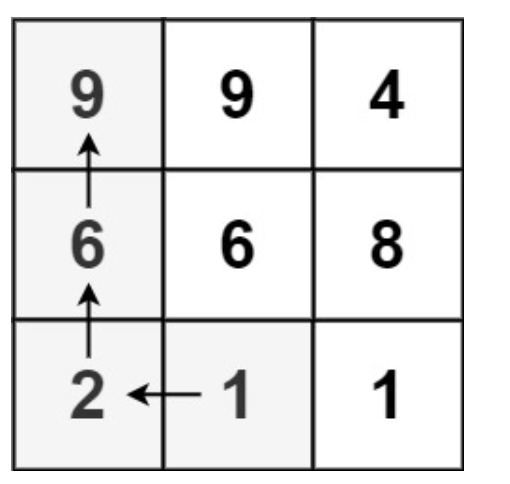
| 输入:matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出:4
解释:最长递增路径为 [1, 2, 6, 9]。
|
示例 2:
1
2
3
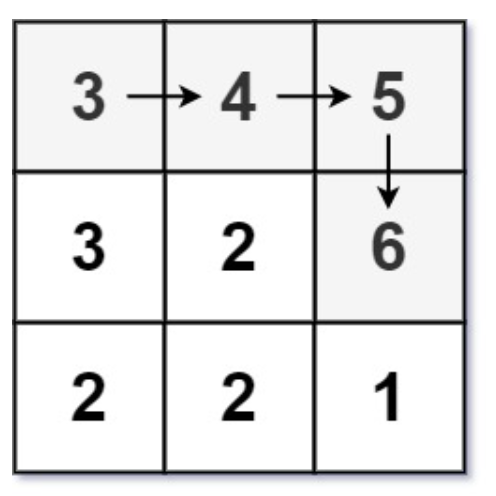
| 输入:matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出:4
解释:最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。
|
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 2000 <= matrix[i][j] <= 2^31 - 1
思路
最朴素的方法为依次$dfs$每个点,找到从每个点开始的最长递增路径的最大值,然后求$max$。
记忆化$dfs$:由于朴素$dfs$会对同一路径进行大量重复操作,时间复杂度为指数级别。我们可以用$f[i][j]$记录从(i,j)出发可以得到的最长递增路径。下次$dfs$到这个坐标可以直接拿来用。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| class Solution {
public:
int n,m;
int ans=0;
int f[210][210];
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
int dfs(vector<vector<int>>& matrix,int x,int y){
if(f[x][y]){
return f[x][y];
}
f[x][y]=1;
for(int i=0;i<4;i++){
int xx=x+dx[i];
int yy=y+dy[i];
if(xx>=0&&xx<n&&yy>=0&&yy<m&&matrix[xx][yy]>matrix[x][y]){
f[x][y]=max(f[x][y],dfs(matrix,xx,yy)+1);
}
}
return f[x][y];
}
int longestIncreasingPath(vector<vector<int>>& matrix) {
n=matrix.size();
m=matrix[0].size();
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
ans=max(ans,dfs(matrix,i,j));
}
}
return ans;
}
};
|
时间复杂度:$O(mn)$,$n$为矩阵的行数,$m$为矩阵的列数。在$dfs$中,时间复杂度为$O(V+E)$,$V$为结点数,$E$为边数$O(V)=O(mn)$,$O(E)\approx O(4mn)$,每个点上下左右四条边。
空间复杂度:$O(mn)$



