Trace
第264场周赛D 并行课程 III
传送门:https://leetcode-cn.com/problems/parallel-courses-iii/
Problem
给你一个整数 n ,表示有 n 节课,课程编号从 1 到 n 。同时给你一个二维整数数组 relations ,其中 relations[j] = [prevCoursej, nextCoursej] ,表示课程 prevCoursej 必须在课程 nextCoursej 之前 完成(先修课的关系)。同时给你一个下标从 0 开始的整数数组 time ,其中 time[i] 表示完成第 (i+1) 门课程需要花费的 月份 数。
请你根据以下规则算出完成所有课程所需要的 最少 月份数:
- 如果一门课的所有先修课都已经完成,你可以在 任意 时间开始这门课程。
- 你可以 同时 上 任意门课程 。
请你返回完成所有课程所需要的 最少 月份数。
注意:测试数据保证一定可以完成所有课程(也就是先修课的关系构成一个有向无环图)。
示例 1:
1
2
3
4
5
6
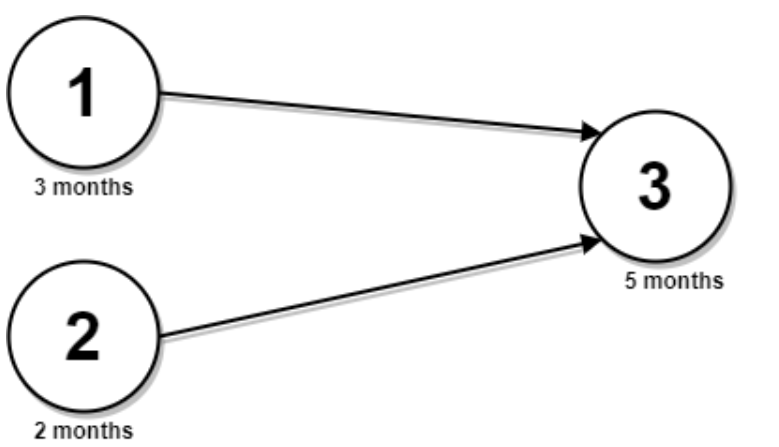
| 输入:n = 3, relations = [[1,3],[2,3]], time = [3,2,5]
输出:8
解释:上图展示了输入数据所表示的先修关系图,以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 和 2 。
课程 1 花费 3 个月,课程 2 花费 2 个月。
所以,最早开始课程 3 的时间是月份 3 ,完成所有课程所需时间为 3 + 5 = 8 个月。
|
示例 2:
1
2
3
4
5
6
7
8
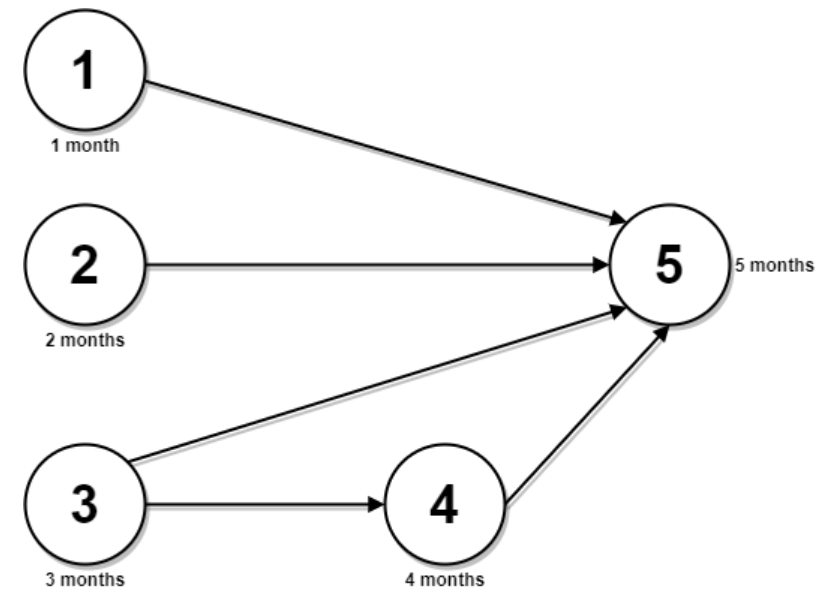
| 输入:n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5]
输出:12
解释:上图展示了输入数据所表示的先修关系图,以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 ,2 和 3 。
在月份 1,2 和 3 分别完成这三门课程。
课程 4 需在课程 3 之后开始,也就是 3 个月后。课程 4 在 3 + 4 = 7 月完成。
课程 5 需在课程 1,2,3 和 4 之后开始,也就是在 max(1,2,3,7) = 7 月开始。
所以完成所有课程所需的最少时间为 7 + 5 = 12 个月。
|
提示:
1 <= n <= 5 * 1040 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)
relations[j].length == 2
1 <= prevCoursej, nextCoursej <= n
prevCoursej != nextCoursej
所有的先修课程对 [prevCoursej, nextCoursej] 都是 互不相同 的。
time.length == n
1 <= time[i] <= 104
先修课程图是一个有向无环图。
思路
满足拓扑序列的情况下,找出最长的一条路径就是答案。
可以用数组$f[i]$来记录到达当前节点的最长距离。
拓扑排序基础题:
https://www.aben.fun/2021/10/25/%E6%9C%89%E5%90%91%E5%9B%BE%E7%9A%84%E6%8B%93%E6%89%91%E5%BA%8F%E5%88%97/
程序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| class Solution {
public:
vector<int> e[50010];
int d[50010];
int f[50010];
int ans=0;
void bfs(int n,vector<int>& time){
queue<int> q;
for(int i=1;i<=n;i++){
if(d[i]==0){
q.push(i);
f[i]=time[i-1];
ans=max(ans,f[i]);
}
}
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=0;i<e[u].size();i++){
int v=e[u][i];
d[v]--;
f[v]=max(f[v],f[u]+time[v-1]);
ans=max(ans,f[v]);
if(d[v]==0){
q.push(v);
}
}
}
}
int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time) {
for(int i=0;i<relations.size();i++){
int u=relations[i][0];
int v=relations[i][1];
e[u].push_back(v);
d[v]++;
}
bfs(n,time);
return ans;
}
};
|



