统计子岛屿

第246场周赛 C

传送门：https://leetcode-cn.com/problems/er-jin-zhi-zhong-1de-ge-shu-lcof/

Problem

给你两个 m x n 的二进制矩阵 grid1 和 grid2 ，它们只包含 0 （表示水域）和 1 （表示陆地）。一个 岛屿 是由 四个方向 （水平或者竖直）上相邻的 1 组成的区域。任何矩阵以外的区域都视为水域。

如果 grid2 的一个岛屿，被 grid1 的一个岛屿 完全 包含，也就是说 grid2 中该岛屿的每一个格子都被 grid1 中同一个岛屿完全包含，那么我们称 grid2 中的这个岛屿为 子岛屿 。

请你返回 grid2 中 子岛屿 的 数目 。

示例 1

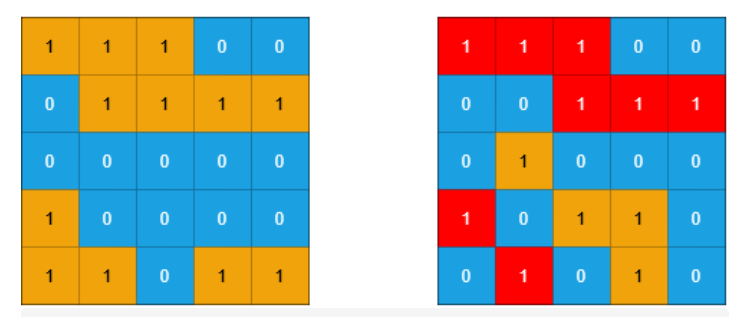
输入：grid1 = [[1,1,1,0,0],[0,1,1,1,1],[0,0,0,0,0],[1,0,0,0,0],[1,1,0,1,1]], grid2 = [[1,1,1,0,0],[0,0,1,1,1],[0,1,0,0,0],[1,0,1,1,0],[0,1,0,1,0]]
输出：3
解释：如上图所示，左边为 grid1 ，右边为 grid2 。
grid2 中标红的 1 区域是子岛屿，总共有 3 个子岛屿。

示例 2

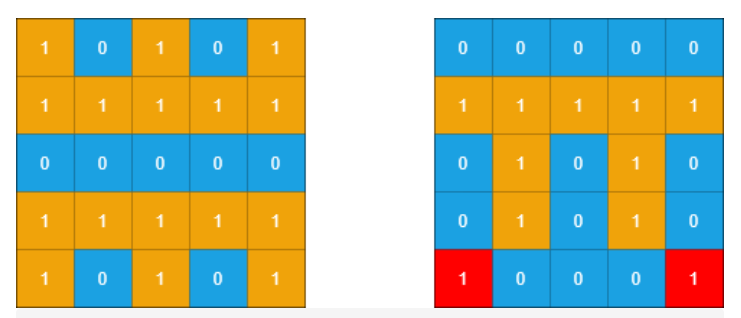
输入：grid1 = [[1,0,1,0,1],[1,1,1,1,1],[0,0,0,0,0],[1,1,1,1,1],[1,0,1,0,1]], grid2 = [[0,0,0,0,0],[1,1,1,1,1],[0,1,0,1,0],[0,1,0,1,0],[1,0,0,0,1]]
输出：2 
解释：如上图所示，左边为 grid1 ，右边为 grid2 。
grid2 中标红的 1 区域是子岛屿，总共有 2 个子岛屿。

数据范围

m == grid1.length == grid2.length
n == grid1[i].length == grid2[i].length
1 <= m, n <= 500
grid1[i][j] 和 grid2[i][j] 都要么是 0 要么是 1 。

思路：

对grid2中的某一个连通块，如果其中的每一个位置在grid1中都为1，那么ans++；（满足此性质的连通块在grid1中也一定是联通的。）

$FloodFill$搭配$bfs$和$dfs$应该都可以，用$dfs$。

class Solution {
public:
    int col;
    int row;
    int count=0;
    int dx[4]={0,0,1,-1};
    int dy[4]={1,-1,0,0};
    // bool vis[501][501]; 不需要vis，可以直接使用g2来判断vis，走过的话将g2[i][j]=0;
    vector<vector<int>> g1,g2;
    bool dfs(int x,int y){
        // 访问到某一个点
        // g2标记访问过
        g2[x][y]=0;
        int flag=true;
        // 判断g1中是否为1
        if(!g1[x][y]) flag=false;
        for(int i=0;i<4;i++){   
            x=x+dx[i];
            y=y+dy[i];
            if(x>=0&&x<row&&y>=0&&y<col&&g2[x][y]){
                if(!dfs(x,y))
                    flag=false;
            }
            x=x-dx[i];
            y=y-dy[i];
        }
        return flag;
    }
    int countSubIslands(vector<vector<int>>& grid1, vector<vector<int>>& grid2) {
        // 思路：对grid2中的某一个连通块，如果其中的每一个位置在grid1中都为1，那么ans++；（满足此性质的连通块在grid1中也一定是联通的。
        g1=grid1;
        g2=grid2;
        col=g2[0].size();
        row=g2.size();
        for(int i=0;i<row;i++){
            for(int j=0;j<col;j++){
                if(g2[i][j]==1){
                    if(dfs(i,j)){
                        count++;
                    };
                }
            }
        }
        return count;
    }
};