Trace
6.16 每日一题
传送门:https://leetcode-cn.com/problems/stone-game/
Problem
亚历克斯和李用几堆石子在做游戏。偶数堆石子排成一行,每堆都有正整数颗石子 piles[i] 。
游戏以谁手中的石子最多来决出胜负。石子的总数是奇数,所以没有平局。
亚历克斯和李轮流进行,亚历克斯先开始。 每回合,玩家从行的开始或结束处取走整堆石头。 这种情况一直持续到没有更多的石子堆为止,此时手中石子最多的玩家获胜。
假设亚历克斯和李都发挥出最佳水平,当亚历克斯赢得比赛时返回 true ,当李赢得比赛时返回 false 。
示例:
1
2
3
4
5
6
7
8
| 输入:[5,3,4,5]
输出:true
解释:
亚历克斯先开始,只能拿前 5 颗或后 5 颗石子 。
假设他取了前 5 颗,这一行就变成了 [3,4,5] 。
如果李拿走前 3 颗,那么剩下的是 [4,5],亚历克斯拿走后 5 颗赢得 10 分。
如果李拿走后 5 颗,那么剩下的是 [3,4],亚历克斯拿走后 4 颗赢得 9 分。
这表明,取前 5 颗石子对亚历克斯来说是一个胜利的举动,所以我们返回 true 。
|
数据范围
1
2
3
4
| 2 <= piles.length <= 500
piles.length 是偶数。
1 <= piles[i] <= 500
sum(piles) 是奇数。
|
dfs
如果数据范围小一点,可以$dfs$。
博弈论
因为$piles.length$是偶数,所以可以把$piles$分为奇数项和偶数项,所以在每一个回合,先手玩家可以限制后手玩家只能取(奇数项/偶数项)。
因此只需要提前比较奇数项和与偶数项和的大小,先手玩家选择较大的就好,从而先手必胜。
1
2
3
4
5
6
| class Solution {
public:
bool stoneGame(vector<int>& piles) {
return true;
}
};
|
区间dp
每次拿石头均从最左侧或最右侧拿,所以保证剩下的石子堆是连续的,可以划分为更小的子问题。
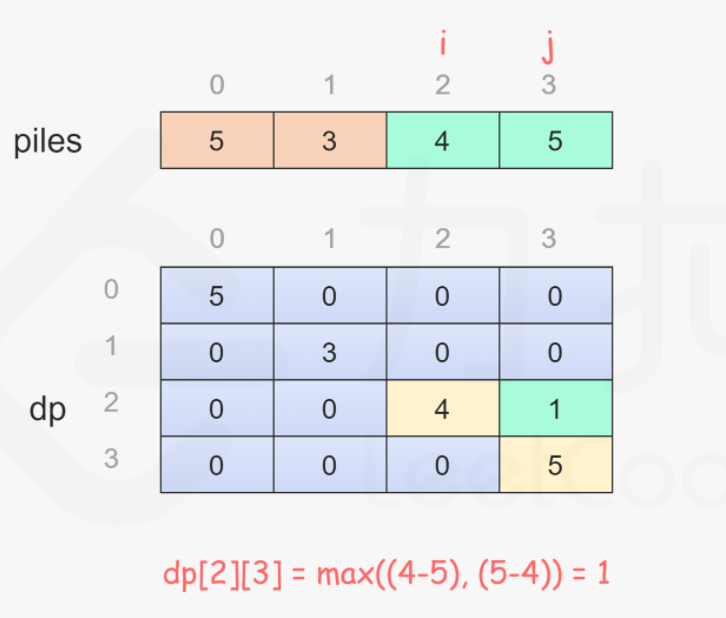
$f[i][j]$:区间$[i,j]$的石子赢取的最大差值。
初始化
$i>j$时没有意义,初始化为0;
$i=j$时,$f[i][j]=piles[i]$,取第$i$堆石子可以拿到最大差值;
状态转移
$f[i][j]=max(piles[i]-f[i+1,j],piles[j]-f[i,j-1])$;
因为每个人每次都要做最优决策,而状态转移$f[i][j]$的状态又是由相邻的状态转移来的,相邻的状态是对手的最优决策,所以计算时做减法。
区间dp写法
1、先枚举长度,再枚举左端点(右端点由左端点和长度计算得来)。
2、先枚举左端点,再枚举右端点(注意枚举顺序,保证状态更新时用到的状态在之前已经计算过/保证结果在最后推出)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
public:
int f[501][501];
bool stoneGame(vector<int>& piles) {
for(int i=0;i<piles.size();i++){
for(int j=0;j<i;j++){
f[i][j]=0;
}
}
for(int i=0;i<piles.size();i++){
f[i][i]=piles[i];
}
for(int len=2;len<=piles.size();len++){
for(int l=0;l+len-1<piles.size();l++){
int r=l+len-1;
f[l][r]=max(piles[l]-f[l+1][r],piles[r]-f[l][r-1]);
}
}
if(f[0][piles.size()-1]>0) return true;
return false;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution {
public:
int f[501][501];
bool stoneGame(vector<int>& piles) {
for(int i=0;i<piles.size();i++){
for(int j=0;j<i;j++){
f[i][j]=0;
}
}
for(int i=0;i<piles.size();i++){
for(int j=0;j<piles.size();j++){
if(i==j){
f[i][j]=piles[i];
}
}
}
for(int i=piles.size()-2;i>=0;i--){
for(int j=i+1;j<piles.size();j++){
f[i][j]=max(piles[i]-f[i+1][j],piles[j]-f[i][j-1]);
}
}
return f[0][piles.size()]>=0?true:false;
}
};
|
空间优化
因为每个状态只和左边和下边的状态有关,可以将动态规划的空间优化为一维$f[501]$。
原转移:
f[i][j]=max(piles[i]-f[i+1][j],piles[j]-f[i][j-1]);
压缩后转移:
f[j]=max(piles[i]-f[j],piles[j]-f[j-1]);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public:
int f[501];
bool stoneGame(vector<int>& piles) {
for(int i=0;i<piles.size();i++){
f[i]=piles[i];
}
for(int i=piles.size()-2;i>=0;i--){
for(int j=i+1;j<piles.size();j++){
f[j]=max(piles[i]-f[j],piles[j]-f[j-1]);
}
}
return f[piles.size()]>=0?true:false;
}
};
|


